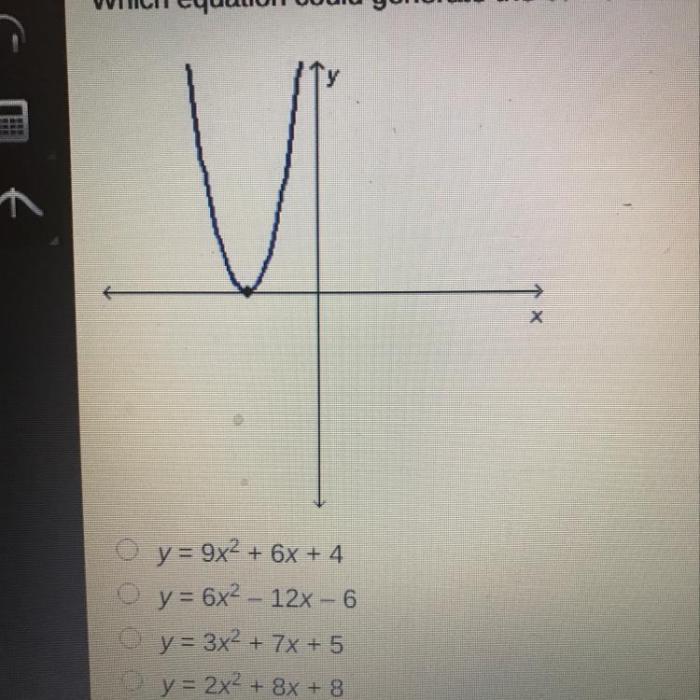
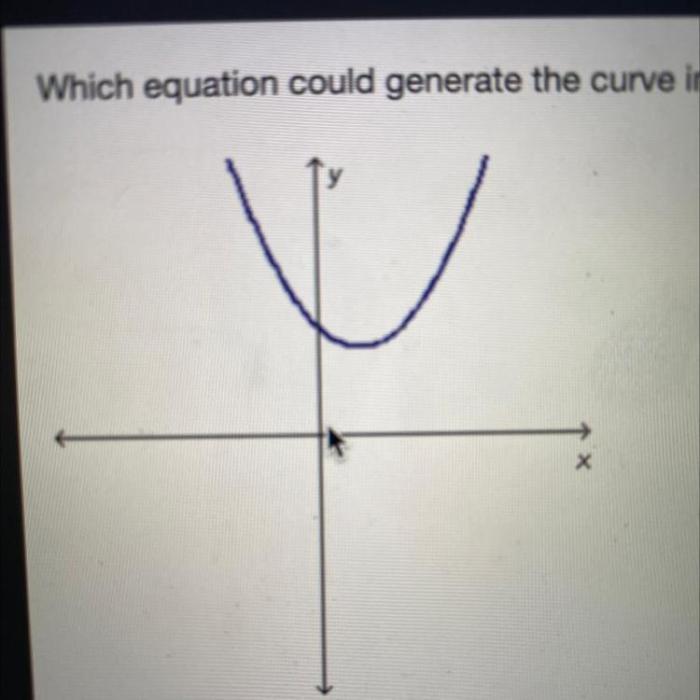
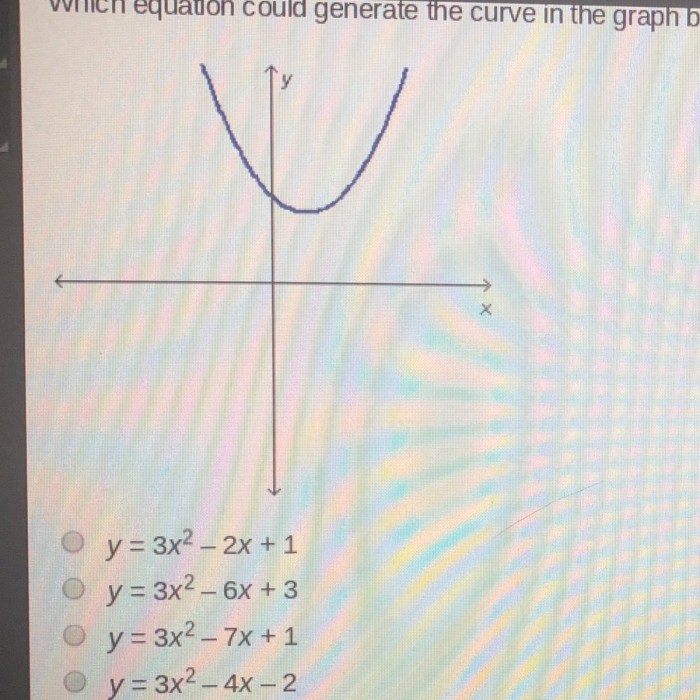
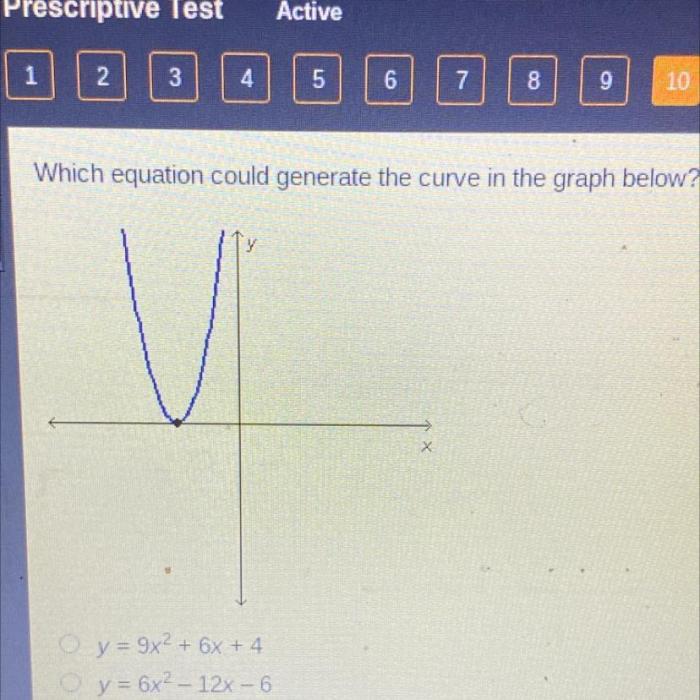
Which equation could generate the curve in the graph below? This question takes center stage in this comprehensive exploration of the relationship between equations and curves. Delving into the intricacies of various curve types, we unravel the parameters and variables that shape their distinctive forms.
Matching equations to graphs requires a keen understanding of curve characteristics, including slopes, intercepts, and asymptotes. This guide provides a systematic approach to identifying the equation that corresponds to a given curve, empowering readers to decipher the language of graphs.
Equations for Generating Curves
Equations play a crucial role in generating and describing curves. Various types of curves can be generated using specific equations, each with its own characteristics and parameters that influence the shape and behavior of the curve.
Linear Equations
Linear equations are of the form y = mx + c, where m is the slope and c is the y-intercept. These equations generate straight lines that exhibit a constant rate of change.
Quadratic Equations
Quadratic equations are of the form y = ax^2 + bx + c, where a, b, and c are constants. These equations generate parabolas, which are U-shaped curves with a vertex at the point (-b/2a, f(-b/2a)).
Exponential Equations
Exponential equations are of the form y = ab^x, where a is a constant and b is the base. These equations generate exponential curves that increase or decrease rapidly, depending on whether b is greater or less than 1, respectively.
Trigonometric Equations, Which equation could generate the curve in the graph below
Trigonometric equations are of the form y = A sin(Bx + C) or y = A cos(Bx + C), where A, B, and C are constants. These equations generate periodic curves that oscillate between a maximum and minimum value.
Matching Equations to Graphs
To identify which equation could generate a given curve, it is essential to analyze its characteristics. The slope, intercepts, and asymptotes of a curve provide valuable clues about the underlying equation.
For example, a straight line with a positive slope indicates a linear equation. A parabola with a vertex opening upwards suggests a quadratic equation with a positive leading coefficient. An exponential curve that increases rapidly indicates a base greater than 1, while a periodic curve with a maximum and minimum value points towards a trigonometric equation.
Examples and Applications
The relationship between equations and curves finds applications in numerous fields. In physics, equations are used to describe the trajectory of objects in motion. In engineering, they are employed to design structures and analyze stresses. In economics, they are utilized to model market behavior and predict trends.
| Equation | Graph |
|---|---|
| y = 2x + 1 | Straight line |
y = x^2
|
Parabola |
| y = 2^x | Exponential curve |
| y = sin(x) | Periodic curve |
Advanced Considerations
Beyond basic equations, parametric equations can be used to generate more complex curves. These equations involve multiple variables and generate curves that can vary in shape and behavior depending on the values of the parameters.
Computer software and graphing tools are invaluable for analyzing equations and generating curves. They allow for the visualization of complex functions and the exploration of different parameters and variables.
Interactive Demonstration
To enhance understanding, an interactive online tool can be designed that allows users to input an equation and see the corresponding graph. This tool can include options to adjust the parameters of the equation and observe how the graph changes.
Such a tool provides a practical way to explore the relationship between equations and curves and gain a deeper understanding of their properties and applications.
Popular Questions: Which Equation Could Generate The Curve In The Graph Below
What are the different types of curve equations?
Curve equations can be linear, quadratic, exponential, trigonometric, or parametric, each with its unique characteristics and applications.
How do I identify the equation that generates a given curve?
By analyzing the curve’s slope, intercept, and asymptotes, you can narrow down the possible equations and determine the most likely candidate.
What are parametric equations used for?
Parametric equations allow us to describe more complex curves by defining the x and y coordinates as functions of a parameter.

